Ergodic process
In signal processing, a stochastic process is said to be ergodic if its statistical properties (such as its mean and variance) can be deduced from a single, sufficiently long sample (realization) of the process.
Contents |
Specific definitions
One can discuss the ergodicity of various properties of a stochastic process. For example, a wide-sense stationary process 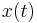 has mean
has mean ![\mu = E[x(t)]](/2012-wikipedia_en_all_nopic_01_2012/I/a33f6e9d71562db42230c68de6b9966f.png) and autocovariance
and autocovariance ![r_x(\tau) = E[(x(t)-\mu) (x(t%2B\tau)-\mu)]](/2012-wikipedia_en_all_nopic_01_2012/I/7f134e97a6142b1d9da83b2b0aa0eb98.png) which do not change with time. One way to estimate the mean is to perform a time average:
which do not change with time. One way to estimate the mean is to perform a time average:
If 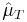 converges in squared mean to
converges in squared mean to  as
as 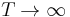 , then the process
, then the process 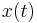 is said to be mean-ergodic[1] or mean-square ergodic in the first moment.[2]
is said to be mean-ergodic[1] or mean-square ergodic in the first moment.[2]
Likewise, one can estimate the autocovariance 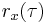 by performing a time average:
by performing a time average:
If this expression converges in squared mean to the true autocovariance ![r_x(\tau) = E[(x(t)-\mu) (x(t%2B\tau)-\mu)]](/2012-wikipedia_en_all_nopic_01_2012/I/7f134e97a6142b1d9da83b2b0aa0eb98.png) , then the process is said to be autocovariance-ergodic or mean-square ergodic in the second moment.[2]
, then the process is said to be autocovariance-ergodic or mean-square ergodic in the second moment.[2]
A process which is ergodic in the first and second moments is sometimes called ergodic in the wide sense.[2]
See also
- Poincaré recurrence theorem
- Loschmidt's paradox
- Ergodic theory, a branch of mathematics concerned with a more general formulation of ergodicity
- Ergodic hypothesis
- Ergodicity
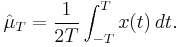
![\hat{r}_x(\tau) = \frac{1}{2T} \int_{-T}^{T} [x(t%2B\tau)-\mu] [x(t)-\mu] \, dt.](/2012-wikipedia_en_all_nopic_01_2012/I/eeec1ff1807b3df7154e92ece4a104bc.png)